Overlap–save method

Overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal x[n] and a finite impulse response (FIR) filter h[n]:

y[n] = x[n] * h[n] \ \stackrel{\mathrm{def}}{=} \ \sum_{m=-\infty}^{\infty} h[m] \cdot x[n-m] = \sum_{m=1}^{M} h[m] \cdot x[n-m], \,

 

 

 

 

(Eq.1)

where h[m]=0 for m outside the region [1, M].

The concept is to compute short segments of y[n] of an arbitrary length L, and concatenate the segments together. Consider a segment that begins at n = kL + M, for any integer k, and define:

x_k[n] \ \stackrel{\mathrm{def}}{=} \begin{cases} x[n%2BkL] & 1 \le n \le L%2BM-1\\ 0 & \textrm{otherwise}. \end{cases}
y_k[n] \ \stackrel{\mathrm{def}}{=} \ x_k[n]*h[n]\,

Then, for kL + M  ≤  n  ≤  kL + L + M − 1, and equivalently M  ≤  n − kL  ≤  L + M − 1, we can write:

\begin{align} y[n] = \sum_{m=1}^{M} h[m] \cdot x_k[n-kL-m] &= x_k[n-kL] * h[n] \\ &\stackrel{\mathrm{def}}{=} \ y_k[n-kL]. \end{align}

The task is thereby reduced to computing yk[n], for M  ≤  n  ≤  L + M − 1.

Now note that if we periodically extend xk[n] with period N  ≥  L + M − 1, according to:

x_{k,N}[n] \ \stackrel{\mathrm{def}}{=} \ \sum_{k=-\infty}^{\infty} x_k[n - kN],

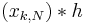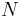the convolutions  (x_{k,N})*h\,  and  x_k*h\,  are equivalent in the region M  ≤  n  ≤  L + M − 1. So it is sufficient to compute the N\,-point circular (or cyclic) convolution of x_k[n]\, with h[n]\,  in the region [1, N].  The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.

The advantage is that the circular convolution can be computed very efficiently as follows, according to the circular convolution theorem:

y_k[n] = \textrm{IFFT}\left(\textrm{FFT}\left(x_k[n]\right)\cdot\textrm{FFT}\left(h[n]\right)\right),

where FFT and IFFT refer to the fast Fourier transform and inverse fast Fourier transform, respectively, evaluated over N discrete points.

Contents

Pseudocode

   (Overlap–save algorithm for linear convolution)
   H = FFT(h,N)
   i = 1
   while i <= Nx
       il = min(i+N-1,Nx)
       yt = IFFT( FFT(x(i:il),N) * H, N)
       y(i : i+N-M) = yt(M : N)
       i = i+N-M+1
   end

Efficiency

The pseudocode above requires about 2N log2(N) + N complex multiplications for the FFT, product of arrays, and IFFT. Each iteration produces N-M+1 output samples, so the number of complex multiplications per output sample is about:

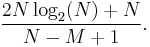
\frac{2N \log_2(N) %2B N}{N-M%2B1}.\,

 

 

 

 

(Eq.2)

For example, when M=201 and N=1024, Eq.2 equals 26, whereas direct evaluation of Eq.1 would require up to 201 complex multiplications per output sample, the worst case being when both x and h are complex-valued. Also note that for any given M, Eq.2 has a minimum with respect to N. It diverges for both small and large block sizes.

Overlap–discard

Overlap–discard and Overlap–scrap are less commonly used labels for the same method described here. However, these labels are actually better (than overlap–save) to distinguish from overlap–add, because both methods "save", but only one discards. "Save" merely refers to the fact that M − 1 input (or output) samples from segment k are needed to process segment k + 1.

Extending overlap–save

The overlap-save algorithm may be extended to include other common operations of a system [1][2]:

Notes

  1. ^ Borgerding 2006, pp 158–161.
  2. ^ Carlin et al. 1999, p 31, col 20.

References